Дробно-рациональная функция

            Формула у = k/ x, графиком является гипербола. В Части 1 ГИА данная функция предлагается без смещений вдоль осей. Поэтому у нее только один параметр k. Самое большое различие во внешнем облике графика зависит от знака k.

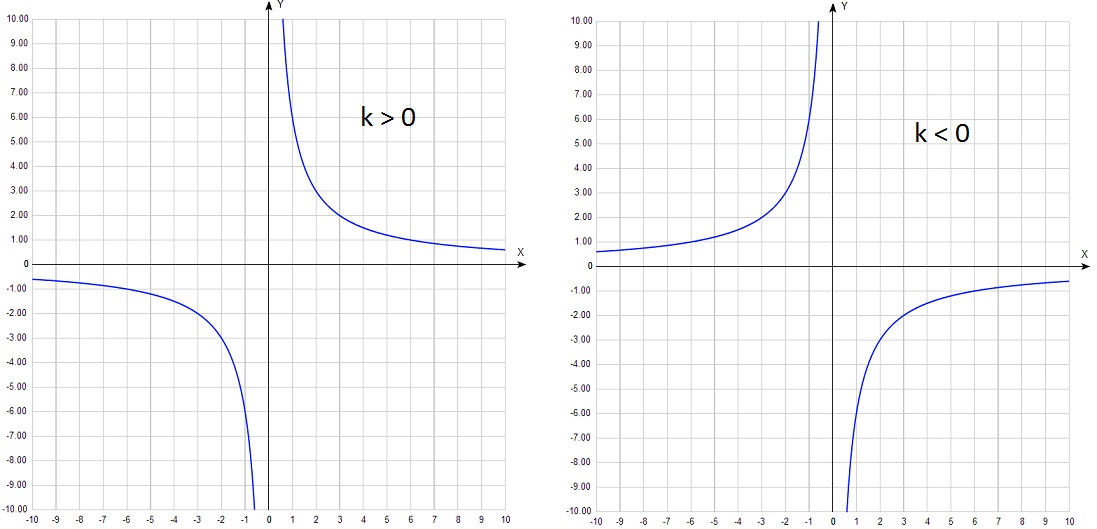
Труднее увидеть отличия в графиках, если k одного знака:

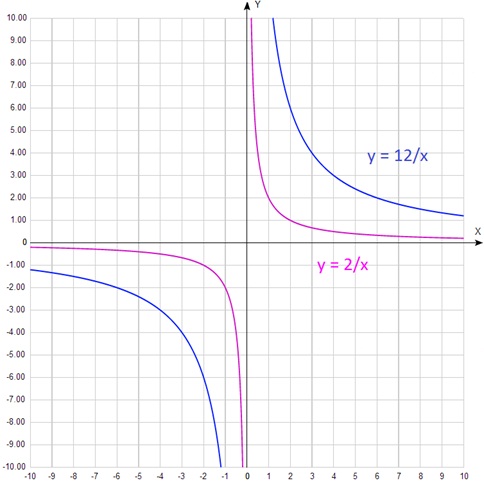
Как мы видим, чем больше k, тем выше проходит гипербола.

На рисунке приведены функции, у которых параметр k отличается существенно. Если же отличие не столь велико, то на глаз определить его достаточно сложно.

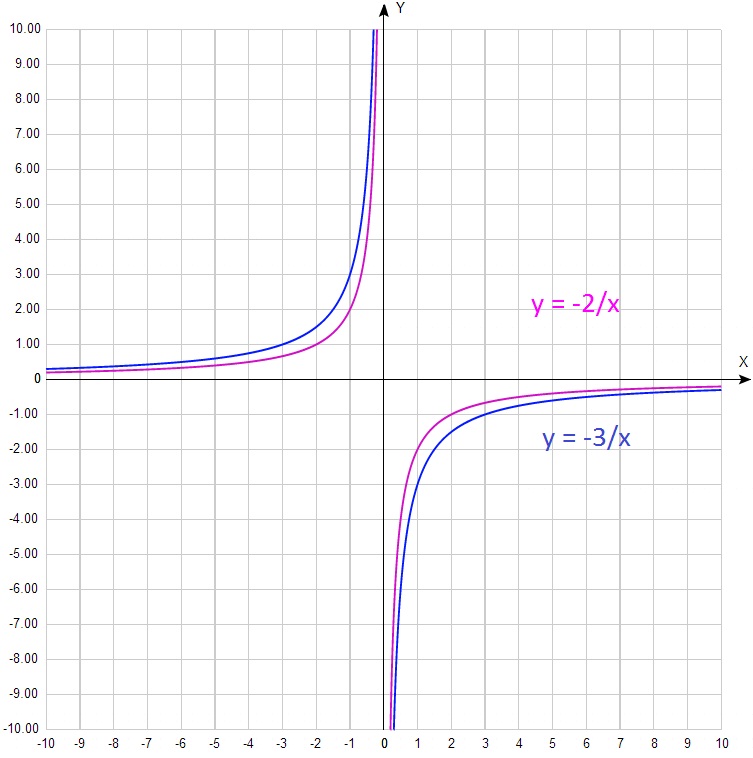
В этом плане просто «шедевром» является следующее задание, обнаруженное мною в неплохом в целом пособии по подготовке к ГИА:

Мало того, что на довольно мелкой картинке близко расположенные графики просто сливаются. Так еще и гиперболы с положительными и отрицательными kизображены в одной координатной плоскости. Что полностью дезориентирует любого, кто взглянет на этот рисунок. В глаза бросается просто «прикольная звездочка».

            Слава Богу, это просто тренировочная задача. В реальных вариантах предлагались более корректные формулировки и очевидные рисунки.

Разберемся, как же определить коэффициент k по графику функции.

            Из формулы: у = k / x следует, что k = у·х. То есть мы можем взять любую целочисленную точку с удобными координатами и перемножить их – получим k.

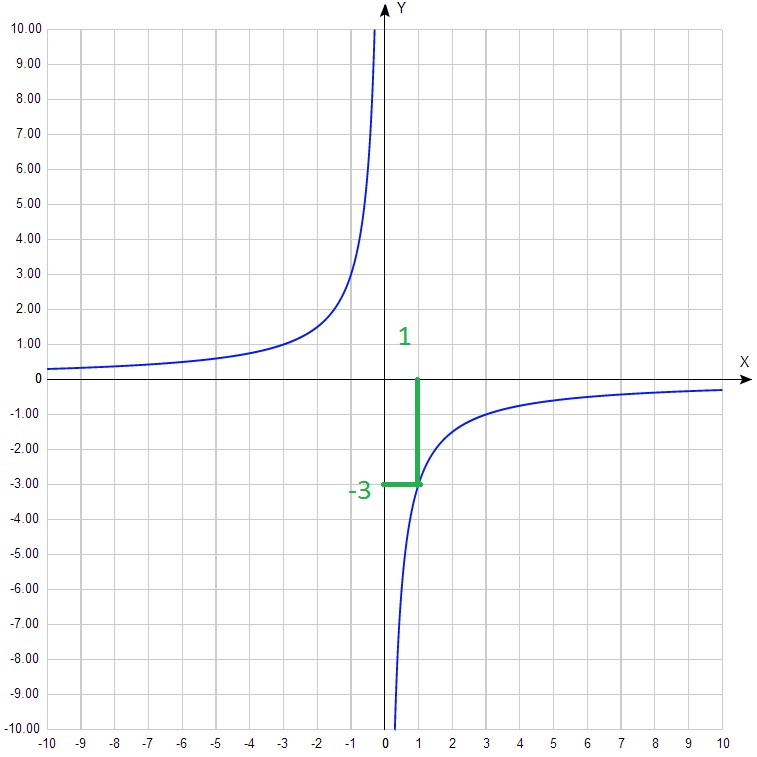
k = 1·(– 3) = – 3.

Следовательно формула этой функции: у = – 3/х.

Интересно рассмотреть ситуацию с дробным k. В этом случае формула может быть записана несколькими способами. Это не должно вводить в заблуждение.

Например, 

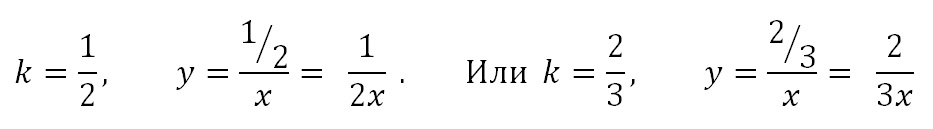
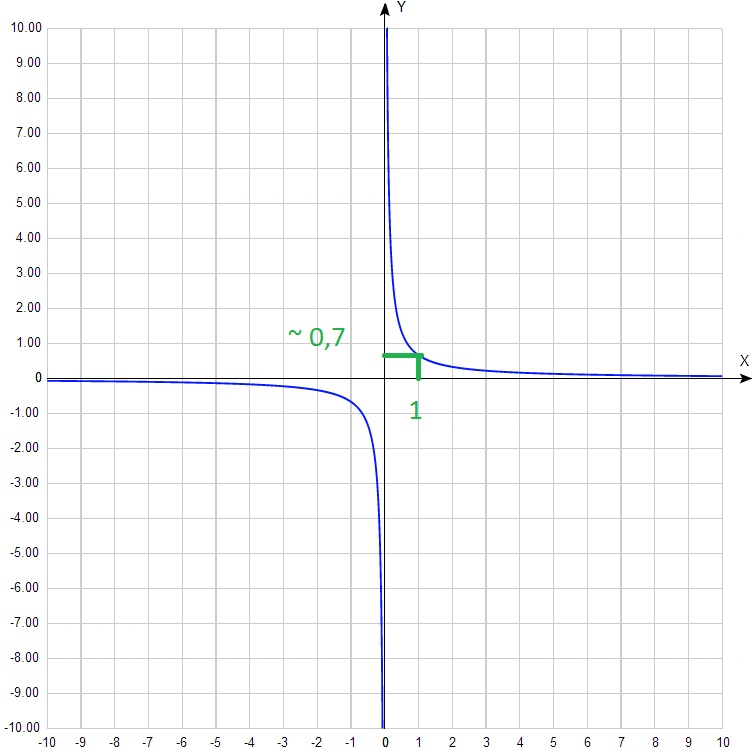
На данном графике невозможно найти ни одной целочисленной точки. Поэтому значение k можно определить весьма приближенно.

k= 1·0,7≈0,7. Однако можно понять, что 0 < k< 1. Если среди предложенных вариантов есть такое значение, то можно считать, что оно и является ответом.

Итак, обобщим.

k > 0 гипербола располагается в 1-й и 3-ем координатных углах (квадрантах),

k < 0 – во 2-м и 4-ом.

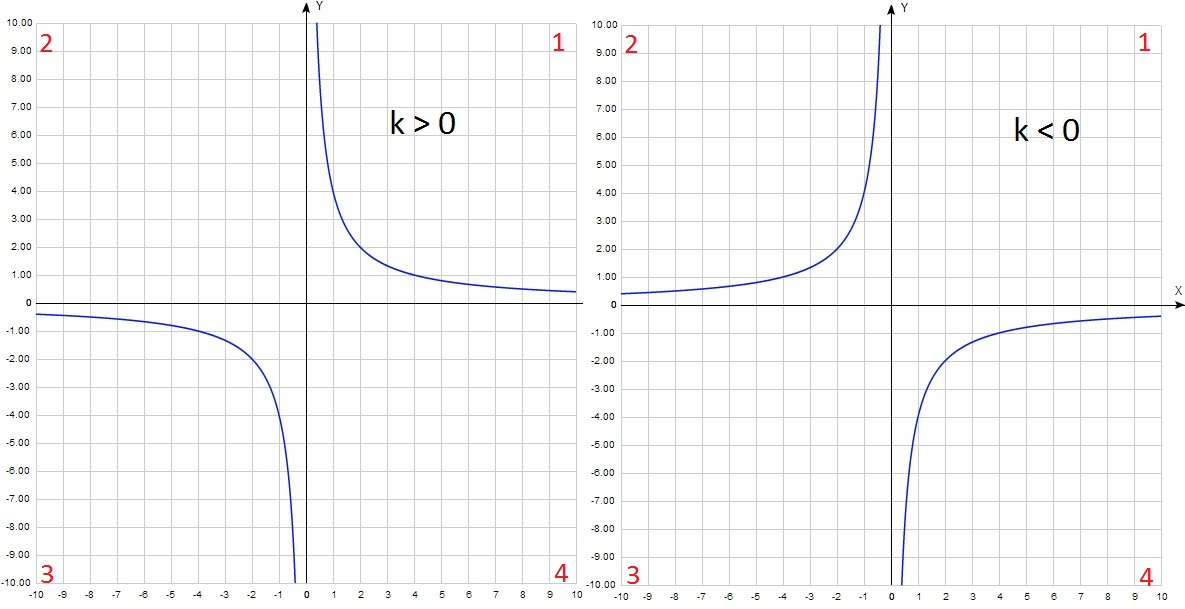
Если k по модулю больше 1 (k = 2 или k = – 2), то график располагается выше 1 (ниже – 1) по оси у, выглядит более широким.

Если k по модулю меньше 1 (k = 1/2 или k = – 1/2), то график располагается ниже 1 (выше – 1) по оси у и выглядит более узким, «прижатым» к нулю:

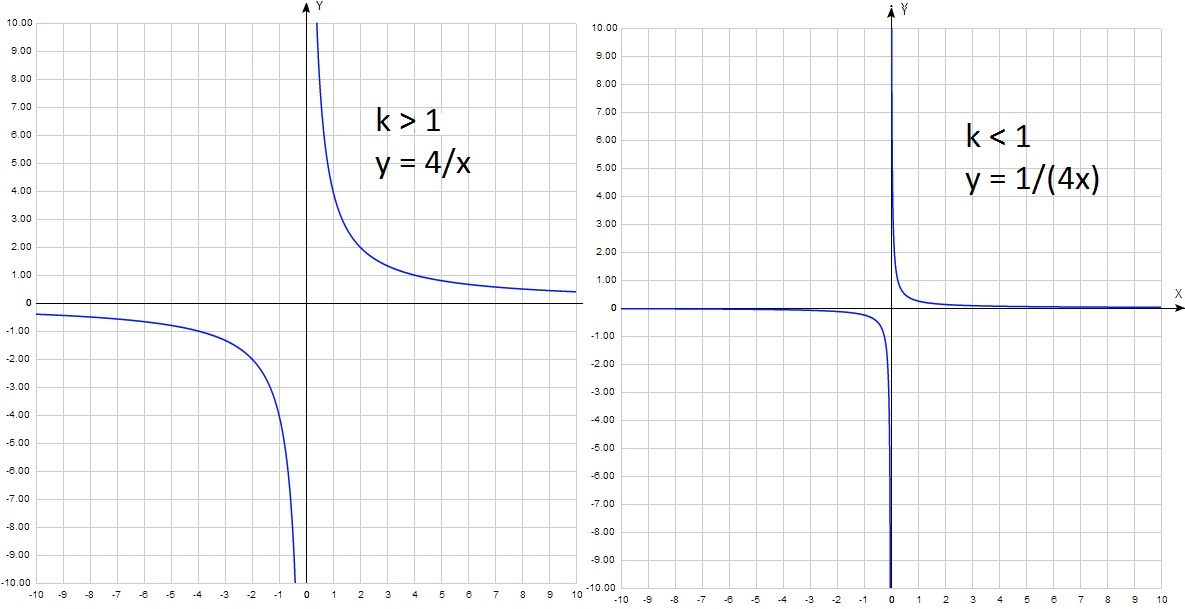
Рассмотрим задачу, предложенную в одном из вариантов ГИА:

ЗАДАЧА:

Установите соответствие между графиками функций и формулами, которые их задают.

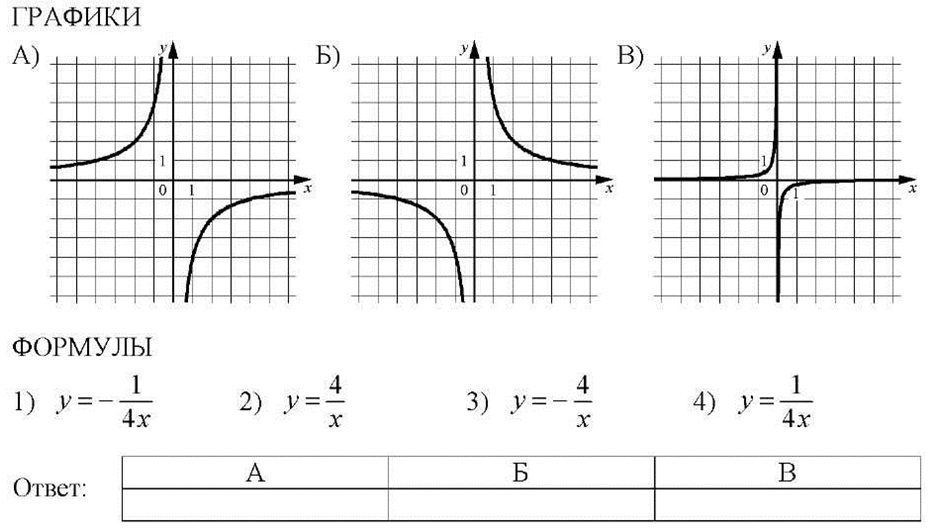
Решение:

А) По расположению гиперболы во втором и четвертом координатных углах можно сделать вывод, что k< 0. Этому условию отвечают формулы 1) и 3). График располагается выше у = 1, поэтому k >1 по модулю, то есть 3)

Б) По расположению гиперболы во первом и третьем координатных углах можно сделать вывод, что k> 0. Этому условию отвечают формулы 2) и 4). График располагается выше у = 1, поэтому k >1 по модулю, то есть 2)

В) По расположению гиперболы во втором и четвертом координатных углах можно сделать вывод, что k< 0. Этому условию отвечают формулы 1) и 3). График располагается ниже у = 1, поэтому k < 1 по модулю, то есть 1)

Ответ:

.

Руслан Александрович - репетитор по математике

тел. моб. (495) 642 42 50. Звонить можно до 23:00. 

тел. моб. 8 (499) 723 68 84. Звонить можно до 23:00.

тел. дом. 8 (925) 642 42 50. Звонить можно до 23:00.

E-mail: mosrepetitor@mail.ru